Also, there's something I've been thinking about for a few days about functions in mathematics that I don't think has any technical merit, just a way of thinking about it, I guess. Not sure if I'm being utterly crackpot with this one though but for some reason, I find it a lot more natural to think about functions in math (in general but not always) as more akin to being "comparisons" between objects, or "associations" than a mechanical device that takes in something, do some operations to it, and spits something else back out, like a C function. The other view isn't wrong of course, and I guess why I started to feel this way is probably because of algebra and topology where it's a lot more natural (I don't know if this is just me) to think about maps between objects as comparisons or associations because then it's a lot easier to see what "structure-preserving" means.
I could be entirely crackpot.
I could be entirely crackpot.
:)
Kou,
you write:
I don't understand. On a number line, it is possible to conceive of many real but irrational numbers in between each rational number. But I thought that only the set of rational numbers, and not real numbers, is countable. So in a finite period of time within a dimension of space (which all would say is equivalent to the number line) Achilles would traverse an uncountably infinite number of points. It seems hard to accept a physical body can perform such a motion. You also say this is accomplished over "infinite periods". But infinite acts completed in a finite time would be the kind of supertask that you talked about later. So I don't see how this is any different than Thompson's Lamp. Can you explain the difference?
you write:
"walking the first half meter takes half a second, the next quarter a quarter of a second, and so on, yielding a finite time divided into countably infinite periods just as the distance walked is divided into countably infinite lengths."
I don't understand. On a number line, it is possible to conceive of many real but irrational numbers in between each rational number. But I thought that only the set of rational numbers, and not real numbers, is countable. So in a finite period of time within a dimension of space (which all would say is equivalent to the number line) Achilles would traverse an uncountably infinite number of points. It seems hard to accept a physical body can perform such a motion. You also say this is accomplished over "infinite periods". But infinite acts completed in a finite time would be the kind of supertask that you talked about later. So I don't see how this is any different than Thompson's Lamp. Can you explain the difference?
Sangui, I think your misunderstanding comes from the assumption that what mathematics studies has to correspond to physical reality, at least in some obvious manner. But this is simply not the case. We don't know if physical space is actually in some sense made up of uncountably many points of "strictly zero size" or if it is fundamentally discrete. But mathematics doesn't care, it simply studies something else. To mathematics, it's not a requirement that there has to be something physical that corresponds to every mathematical idea. We don't have to have some kind of "infinity" in the physical world to justify its existence. The only justification it needs is that it's interesting to study.
:)
i don't know if there's a reply feature on this website but i'm replying to flask. i read about some ring theory and field extension stuff since last time. recently i've been reading just a tiny bit of logic, mainly reading topology. i'm probably gonna be doing that until i'm bored.
:)
Monologue

I'm thinking about a weird construction in topology: the ordered square. Think of it as a square on the ordinary euclidean plane with corners on the points <0, 0> and <1, 1>, boundaries included. We can define an order on the square by comparing two points p, q on that square the following way:
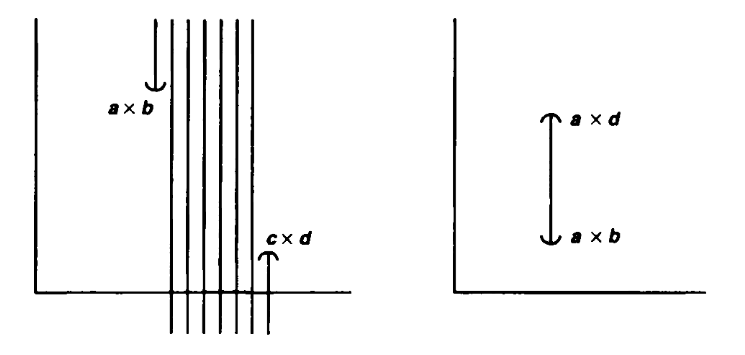
If two points p = <a, b> and q = <c, d> are on the same vertical, i.e., a = c, then we say that p < q if b < d as ordinary real numbers. If the points are not on the same vertical, perhaps we have a < c, then p < q. (Note that even though I'm using the same symbol '<' for order on the square and on the ordinary real numbers, they are different concepts altogether.)
This square as a topological space has the property of connectedness (i.e., informally put, it's "all in one piece") but it doesn't have the property of path-connectedness (i.e., any two points can be connected by a path).

I've been trying to think of an informal explanation for why it's not path-connected. It's easy to see (I think?) that the ordered square is path-connected locally, along every vertical including the boundary points since it has the same order type as the closed interval along verticals. But why is it not true globally? It seems as though any two points on distinct verticals are not path-connected because the closed interval is maybe "too small" to map between the two points. I'm stretching beyond what I actually know here but I think it's because while we may be able to order-embed(?) a closed interval into the ordered square easily along each vertical, we can't do that with endpoints on different verticals, perhaps because between any two verticals, there are uncountably many such verticals. Not even sure if any of these thoughts make sense.
I'm thinking about a weird construction in topology: the ordered square. Think of it as a square on the ordinary euclidean plane with corners on the points <0, 0> and <1, 1>, boundaries included. We can define an order on the square by comparing two points p, q on that square the following way:
If two points p = <a, b> and q = <c, d> are on the same vertical, i.e., a = c, then we say that p < q if b < d as ordinary real numbers. If the points are not on the same vertical, perhaps we have a < c, then p < q. (Note that even though I'm using the same symbol '<' for order on the square and on the ordinary real numbers, they are different concepts altogether.)
This square as a topological space has the property of connectedness (i.e., informally put, it's "all in one piece") but it doesn't have the property of path-connectedness (i.e., any two points can be connected by a path).
I've been trying to think of an informal explanation for why it's not path-connected. It's easy to see (I think?) that the ordered square is path-connected locally, along every vertical including the boundary points since it has the same order type as the closed interval along verticals. But why is it not true globally? It seems as though any two points on distinct verticals are not path-connected because the closed interval is maybe "too small" to map between the two points. I'm stretching beyond what I actually know here but I think it's because while we may be able to order-embed(?) a closed interval into the ordered square easily along each vertical, we can't do that with endpoints on different verticals, perhaps because between any two verticals, there are uncountably many such verticals. Not even sure if any of these thoughts make sense.
:)
I'm reading about presheaves. Hopefully will be reading about sheaves soon. I'll probably update.
I'll also probably write notes and upload them somewhere to the internet in the near-to-medium-term future.
I'll also probably write notes and upload them somewhere to the internet in the near-to-medium-term future.
:)
