I wrote to John Little, one of the authors of Ideals, Varieties, and Algorithms, to obtain a PDF for the solutions to the exercises in his book. Let's see how this goes!!!!!!
:)
More info about Ideals, Varieties, and Algorithms: in my earlier post, I was looking at the third edition of the book and was unaware that there is a fourth edition to this book which has a bit more content. Also forgot to mention that the last appendix is titled "Independent Projects" and lists 14 projects (and a few more) an instructor could give to their students, or a reader could do by themselves. They all quite complex to me to be honest.
:)
Hey, I'm not really knowledgeable about mathematics at all (I only got to discrete math in high school and learned some of linear algebra in college). So I will apologize in advance if this question sounds stupid. Yet I have not seen any kind of concrete answer to this question, and usually people who ask it are dismissed as stupid which I am not going to fall down on either way.
I guess the most succinct way to ask this question would be:
1) How can actual infinities exist, given that
a) the existence of infinity would imply the conclusions of Zeno's paradoxes and those of the Mingjia are true, when they are evidently not;
b) the existence of infinity would fall into many modern paradoxes, like Hilbert's paradox of the hotel or the light switch paradox;
2) If actual infinities do exist, how can one infinity be "greater" than another given the comparative operators are equivalent to the positivity or negativity of the result of a subtraction operation on the comparands, but infinite numbers cannot be subtracted from each other, therefore there is no solution to the comparison
3) What is the proof for actual infinities? If the existence of actual infinites cannot be derived from the axioms of whatever theory, it is just a philosophical assumption that seems to lack any kind of supporting evidence.
SO again, I am not trying to ask a stupid question, but if it is a stupid question, you can also say so.
I guess the most succinct way to ask this question would be:
1) How can actual infinities exist, given that
a) the existence of infinity would imply the conclusions of Zeno's paradoxes and those of the Mingjia are true, when they are evidently not;
b) the existence of infinity would fall into many modern paradoxes, like Hilbert's paradox of the hotel or the light switch paradox;
2) If actual infinities do exist, how can one infinity be "greater" than another given the comparative operators are equivalent to the positivity or negativity of the result of a subtraction operation on the comparands, but infinite numbers cannot be subtracted from each other, therefore there is no solution to the comparison
3) What is the proof for actual infinities? If the existence of actual infinites cannot be derived from the axioms of whatever theory, it is just a philosophical assumption that seems to lack any kind of supporting evidence.
SO again, I am not trying to ask a stupid question, but if it is a stupid question, you can also say so.
"paradox" has several different meanings, among them the idea of a "self-contradiction" (antinomy) as well as "an unintuitive axiomatic consequence" (veridical/falsidical paradox). it's crucial to understand which any given paradox is; zeno's dichotomy paradox and thomson's lamp are the first kind and hilbert's grand hotel is the second kind. if your question is if the concept of infinities map to anything physically, the truth is that it's unknown. it's unknown if the universe is finite or infinite in size and should it be infinite it's unknown if it would be countably or uncountably infinite. in either case infinity remains a useful conceptual tool which we take as an axiom from set theory, but by definition that is something that is taken to be true without any prior, and implies nothing about the physical realm.
zeno's paradoxes--all of which are roughly equivalent--are specifically falsidical paradoxes, that is to say that they are fallacious in nature. it is what some would call a supertask, and the feasibility of a supertask as described by zeno is demonstrated best by diogenes' solvitur ambulando. walking the first half meter takes half a second, the next quarter a quarter of a second, and so on, yielding a finite time divided into countably infinite periods just as the distance walked is divided into countably infinite lengths.
hilbert's grand hotel is a veridical paradox, in that it's just a consequence of assuming the practical existence of countable infinities.
this leaves us with the final supertask and unresolved paradox of the countably infinite, thomson's lamp, which is indeed problematic to possibility of physical infinities existing and to which i have yet to find a satisfactory resolution.
finally, to answer your question about some infinities being greater than other, the key is to abstract the idea of being "greater than" or "less than" beyond values, where the subtraction method would make sense, and instead think about the cardinalities of sets, the number of items within a set. this is, of course, where set theory intertwines with infinity. how does one compare the cardinality of a set with five items and a set with four items? in set theory this is done with a pairing function; in this case the first four items of each set can be paired, but remaining in the first set is an item that cannot be paired. therefore it must be concluded that the first set has a greater cardinality than the second set and the second set has a lesser cardinality than the first set. this is the foundation of hilbert's grand hotel, that the set of all natural numbers has the same cardinality (what is known as ℵ₀) as the set of all natural numbers twice because one can define a pairing function between them, namely mapping the first half to even numbers and the second half to odd numbers.
the concept of an infinity that is greater than another is explained best with cantor's famous diagonal argument, which elegantly establishes that no pairing function can be established between the set of all natural numbers (a set of cardinality ℵ₀) and all of the real numbers which doesn't fail to pair at least one real number, implying that the cardinality of the set of real numbers (𝔠) is greater than the set of natural numbers.
such is my unerudite understanding, i hope this is of some value.
zeno's paradoxes--all of which are roughly equivalent--are specifically falsidical paradoxes, that is to say that they are fallacious in nature. it is what some would call a supertask, and the feasibility of a supertask as described by zeno is demonstrated best by diogenes' solvitur ambulando. walking the first half meter takes half a second, the next quarter a quarter of a second, and so on, yielding a finite time divided into countably infinite periods just as the distance walked is divided into countably infinite lengths.
hilbert's grand hotel is a veridical paradox, in that it's just a consequence of assuming the practical existence of countable infinities.
this leaves us with the final supertask and unresolved paradox of the countably infinite, thomson's lamp, which is indeed problematic to possibility of physical infinities existing and to which i have yet to find a satisfactory resolution.
finally, to answer your question about some infinities being greater than other, the key is to abstract the idea of being "greater than" or "less than" beyond values, where the subtraction method would make sense, and instead think about the cardinalities of sets, the number of items within a set. this is, of course, where set theory intertwines with infinity. how does one compare the cardinality of a set with five items and a set with four items? in set theory this is done with a pairing function; in this case the first four items of each set can be paired, but remaining in the first set is an item that cannot be paired. therefore it must be concluded that the first set has a greater cardinality than the second set and the second set has a lesser cardinality than the first set. this is the foundation of hilbert's grand hotel, that the set of all natural numbers has the same cardinality (what is known as ℵ₀) as the set of all natural numbers twice because one can define a pairing function between them, namely mapping the first half to even numbers and the second half to odd numbers.
the concept of an infinity that is greater than another is explained best with cantor's famous diagonal argument, which elegantly establishes that no pairing function can be established between the set of all natural numbers (a set of cardinality ℵ₀) and all of the real numbers which doesn't fail to pair at least one real number, implying that the cardinality of the set of real numbers (𝔠) is greater than the set of natural numbers.
such is my unerudite understanding, i hope this is of some value.
in relation to the idea in kou's post regarding distinct infinities arising from comparative set sizes and the notion of the infinitesimal, there are facts about the set of rational numbers you've no doubt encountered while practicing arithmetic that still bewilder me when i think about them but are likely unblinking, boring axioms to those immersed in more complex ideas in set theory
(replace all mention of 'rational numbers' with 'real numbers' in this, i haven't studied math in many years and forgot the difference)
within the set of rational numbers there is an infinite set of numbers between any two numbers in the set. at first this seems absurd because it should be possible to pick a number which is immediately close to the following number; however, the notion of a real infinitesimal number which could be named in the set is disproven by proof of .999... being equal to 1, implying that all numbers within the set which could be argued as being immediately next to the following number are merely the following number by definition
this can seem like a quaint observation once you've accepted these proofs, however what continues to baffle me even to this day is knowing that the entirety of integral and differential calculus as well as their applied subdisciplines are entirely founded on this behavior of the rational numbers applied to the domain of functions in all dimensions. while you cannot actually name an infinitesimal differentiation between the set of rational numbers, you can use the mere idea of such a thing existing by the epsilon-delta method to derive infinitesimal rates of change between two immediately close points on a function throughout the entirety of the function, which is an analytical consequence applied to infinite infinities within an infinite domain. the same applies in like fashion to integration with the infinitesimal area under the function
this probably seems like child's play to anyone smarter than a toad, but i would be lying through my teeth if i didn't admit that the idea of using something nonexistent by definition to prove existent relations between functions is impossibly daunting to me and very difficult to understand beyond nodding along with the conclusions
a question though: in the set of rational numbers, is the infinite set between 1 and 2 less than the infinite set between 1 and 3, or are they the same size? intuitively i would think their magnitude scales according to the finite difference between the bounds of the set, but i don't want to be hasty in drawing a conclusion here from my intuition
(replace all mention of 'rational numbers' with 'real numbers' in this, i haven't studied math in many years and forgot the difference)
within the set of rational numbers there is an infinite set of numbers between any two numbers in the set. at first this seems absurd because it should be possible to pick a number which is immediately close to the following number; however, the notion of a real infinitesimal number which could be named in the set is disproven by proof of .999... being equal to 1, implying that all numbers within the set which could be argued as being immediately next to the following number are merely the following number by definition
this can seem like a quaint observation once you've accepted these proofs, however what continues to baffle me even to this day is knowing that the entirety of integral and differential calculus as well as their applied subdisciplines are entirely founded on this behavior of the rational numbers applied to the domain of functions in all dimensions. while you cannot actually name an infinitesimal differentiation between the set of rational numbers, you can use the mere idea of such a thing existing by the epsilon-delta method to derive infinitesimal rates of change between two immediately close points on a function throughout the entirety of the function, which is an analytical consequence applied to infinite infinities within an infinite domain. the same applies in like fashion to integration with the infinitesimal area under the function
this probably seems like child's play to anyone smarter than a toad, but i would be lying through my teeth if i didn't admit that the idea of using something nonexistent by definition to prove existent relations between functions is impossibly daunting to me and very difficult to understand beyond nodding along with the conclusions
a question though: in the set of rational numbers, is the infinite set between 1 and 2 less than the infinite set between 1 and 3, or are they the same size? intuitively i would think their magnitude scales according to the finite difference between the bounds of the set, but i don't want to be hasty in drawing a conclusion here from my intuition
"I know what I must do, be strong lest I shall perish!" 💪✡

I'm not very well versed mathematically, but from what I assume/understand these infinities would be the same size. For every number from between 1 and 2 you can pick a "paired" number from between 1 and 3, for example by doing 2x-1. As every number from the first set has a pair in the second set, and vice versa by (x+1)/2, these sets would be equal.
This works the same way as the proof of there being an equal amount of natural numbers and even natural numbers, at least if i understood the point of that one correctly.
I'm no mathematician, so please correct me if i'm wrong, but at least to me this makes sense
This works the same way as the proof of there being an equal amount of natural numbers and even natural numbers, at least if i understood the point of that one correctly.
I'm no mathematician, so please correct me if i'm wrong, but at least to me this makes sense
the cardinality of the set of rational numbers between 1-2 and 1-3 is the same (ℵ₀). consider that the cardinality of the set of all even naturals is the same as the cardinality of the set of all naturals; each natural number can be paired with the even number corresponding to its value doubled.
cantor famously demonstrated that the cardinality of the set of all rationals is the same as the cardinality of the set of all natural numbers by establishing a one-to-one correspondence between them (1/1 → 1, 1/2 → 2, 2/1 → 3, 3/1 → 4, ...):

similarly, one may demonstrate that the cardinality of the set of all rationals between 0 and 1 is the same as the cardinality of the set of all natural numbers by establishing a one-to-one correspondence between them (1/1 → 1, 1/2 → 2, 2/2 → 3, 1/3 → 4, ...):
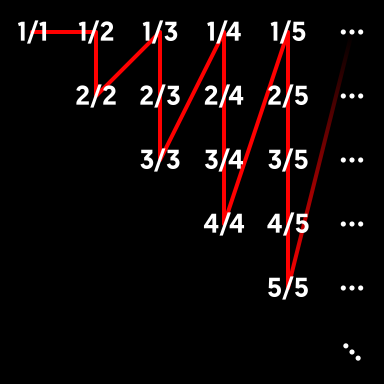
this can be done with any set of rationals between integers, for example 1 to 3, just by prefixing each ratio with the integers in question:

one may also convince themselves that this is a true correspondence by considering the ratios between 1 and 2 as being mapped to the odd naturals and the ratios between 2 and 3 as being mapped to the even naturals, though this is conceptually superfluous.
cantor famously demonstrated that the cardinality of the set of all rationals is the same as the cardinality of the set of all natural numbers by establishing a one-to-one correspondence between them (1/1 → 1, 1/2 → 2, 2/1 → 3, 3/1 → 4, ...):
similarly, one may demonstrate that the cardinality of the set of all rationals between 0 and 1 is the same as the cardinality of the set of all natural numbers by establishing a one-to-one correspondence between them (1/1 → 1, 1/2 → 2, 2/2 → 3, 1/3 → 4, ...):
this can be done with any set of rationals between integers, for example 1 to 3, just by prefixing each ratio with the integers in question:
one may also convince themselves that this is a true correspondence by considering the ratios between 1 and 2 as being mapped to the odd naturals and the ratios between 2 and 3 as being mapped to the even naturals, though this is conceptually superfluous.
Thanks for both of your responses. I will have to think about this matter more before I say anything else.